Understanding Rule of inference in Functional Dependency – A Guide by UpdateGadh
Rule of inference
When working with relational databases, understanding how functional dependencies (FDs) behave is crucial for ensuring data integrity and normalization. One of the most foundational concepts that helps in reasoning about FDs is the set of Inference Rules, famously known as Armstrong’s Axioms.
At UpdateGadh, we’re committed to simplifying core database concepts. In this blog, we’ll break down the six types of inference rules you need to know to master functional dependency in relational databases.
Machine Learning Tutorial:-Click Here
Data Science Tutorial:-Click Here
Complete Advance AI topics:- CLICK HERE
Deep Learning Tutorial:- Click Here
What Are Inference Rules?
From an existing collection, we can infer new functional dependencies using inference rules.These are essentially logical assertions that help database designers analyze and manipulate functional dependencies.
The Armstrong’s Axioms form the basis for these inference rules and are fundamental to relational database theory. Using these rules, we can systematically infer all valid FDs that hold in a given relation.
Six main categories of inference rules exist:
1. Reflexive Rule (IR1)
This rule is quite intuitive. It asserts that X determines Y if a collection of qualities Y is a subset of X.
When X ⊇ Y, X → Y
Example:
Let
X = {a, b, c, d, e}
Y = {a, b, c}
The relationship X → Y is evident as Y is a subset of X.
2. Augmentation Rule (IR2)
Also known as partial dependency, this rule allows us to append additional attributes to both sides of a functional dependency.
If X → Y, then XZ → YZ (for any Z)
Example:
Consider a relation R(A, B, C, D).
If A → B, then by augmentation, AC → BC.
This is useful in maintaining consistency when additional attributes are involved.
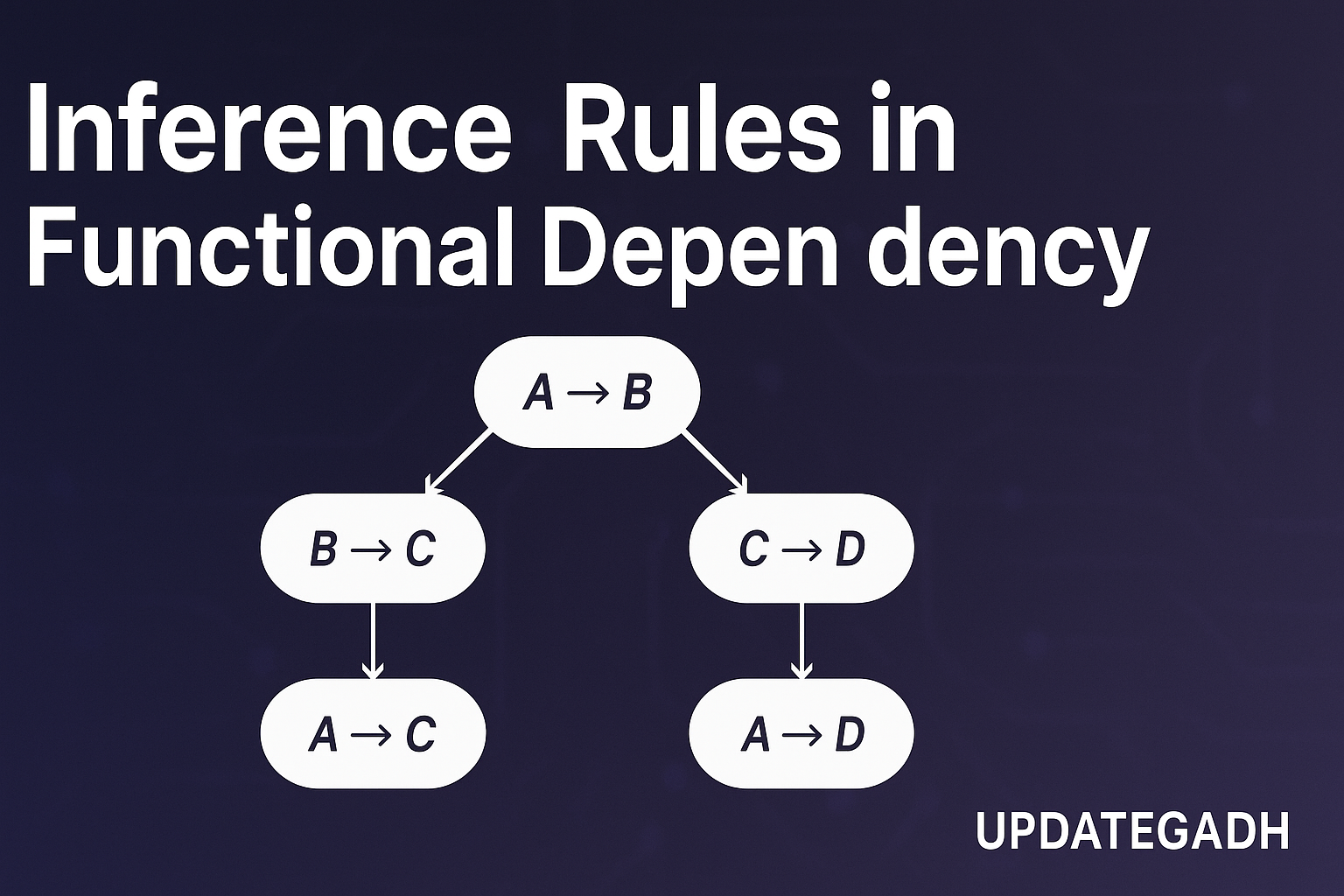
3. Transitive Rule (IR3)
Similar to the transitive property in mathematics, this rule states that if one attribute set determines a second, and that second set determines a third, then the first must determine the third.
If X → Y and Y → Z, then X → Z
Example:
If A → B and B → C, then logically, A → C.
4. Union Rule (IR4)
This rule combines two functional dependencies with the same determinant into a single dependency.
If X → Y and X → Z, then X → YZ
Proof:
- X → Y (Given)
- X → Z (Given)
- X → XY (Using Augmentation on 1)
- XY → YZ (Using Augmentation on 2)
- X → YZ (Using Transitive Rule on 3 and 4)
5. Decomposition Rule (IR5)
Also referred to as the project rule, this is the reverse of the union rule. If a set of attributes determines a combined set, it also determines each component individually.
If X → YZ, then X → Y and X → Z
Proof:
- X → YZ (Given)
- YZ → Y (By Reflexive Rule)
- X → Y (By Transitive Rule using 1 and 2)
Similarly, we can prove X → Z.
6. Pseudo Transitive Rule (IR6)
This rule is slightly more complex but powerful when chaining multiple dependencies with overlapping attributes.
If X → Y and YZ → W, then XZ → W
Proof:
- X → Y (Given)
- YZ → W (Given)
- XZ → YZ (Using Augmentation on 1)
- XZ → W (Using Transitive Rule on 3 and 2)
Complete Python Course with Advance topics:-Click Here
SQL Tutorial :-Click Here
Download New Real Time Projects :-Click here
Conclusion
One of the most important skills in relational database architecture is understanding inference rules.These six rules not only help validate the correctness of functional dependencies but also play a vital role in normalization and schema optimization.
By applying Armstrong’s Axioms—the backbone of these rules—you can confidently derive any valid functional dependency from a given set. At UpdateGadh, we encourage learners and professionals alike to internalize these rules for effective database design.
Stay tuned for more insightful guides from UpdateGadh on database systems and beyond.
rules of inference examples
rule of inference in discrete mathematics
rules of inference exercises with answers
rules of inference pdf
9 rules of inference
rules of inference exercises with answers pdf
rule of inference in ai
simplification rule of inference
rules of inference
de morgan’s law rule of inference
resolution rule of inference
deductive rule of inference
simplification rule of inference
addition rule of inference
conjunction rule of inference
modus ponens rule of inference
simplification rule of inference examples
contrapositive rule of inference
inductive rule of inference
rule of inference addition









Post Comment